Analysis II Lecture 15 Part 1 vector fields on manifolds
Tangent vector fields on smooth manifolds are defined. A smooth homotopy of smooth functions is defined between manifolds. Examples are given. A smooth ...
Arthur Parzygnat
Analysis II Lecture 12 Part 1 the tangent space
The tangent space of Euclidean space (or of an open set in Euclidean space) at a point is a vector space of the same dimension as that Euclidean space.
Arthur Parzygnat
Multi-Variable Calculus: 8.2- Function of Several Variables: Limit and Continuity
Instructor: Saman Habibi Esfahani Multi-Variable Calculus: 8.2- Function of Several Variables: Limit and Continuity July 30, 2020 Stony Brook University, ...
Saman Habibi Esfahani
Legendary Calculus Book from 1922
This a very interesting calculus book that actually cites most of it's exercises. The book is called "A Treatise on the Integral Calculus with Applications, Examples, ...
The Math Sorcerer
Symplectic geometry & classical mechanics, Lecture 2
For winter semester 2017-18 I am giving a course on symplectic geometry and classical mechanics. This course is intended for anyone with a familiarity with ...
Tobias Osborne
Differential forms and integration on manifolds
The theory of integration on manifolds is difficult, partly because there is quite a bit of technical machinery involved to set up differential forms. In this video, we ...
DanielChanMaths
Tensor Calculus 21: Lie Bracket, Flow, Torsion Tensor
Videos on Covariant Derivative: 17 - Flat Space: https://www.youtube.com/watch?v=U5iMpOn5IHw 18 - Curved Surfaces: ...
eigenchris
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors.
XylyXylyX
The THICKEST Advanced Calculus Book Ever
In this video I go over the thickest advanced calculus book I own. This book is thick! How thick? Well it's so thick that sometimes it doesn't stay open unfortunately ...
The Math Sorcerer
Advanced Calculus: differentiation on the manifold examples, 10-2-17, part 1
James Cook
Manifolds
This video will look at the idea of a manifold and how it is formally defined. It will also provide an example of a change of coordinates as a mapping between ...
Tensor Calculus - Robert Davie
Math 032 Multivariable Calculus 09 100314: Linearization and Differentiability
Tangent plane; linearization of a function of two variables; matrix multiplication; using the linearization to approximate the function; differentiability.
Winston Ou
calculus of several variables(21):Implicit differentiation
Implicit differentiation for functions of several variables.
Yuwen Luo
Analysis II Lecture 11 Part 3 implicitly defined manifolds
Implicitly defined manifolds are manifolds that are defined as level sets of functions. The critical points, regular values, and regular points of a differentiable ...
Arthur Parzygnat
Tensor Calculus 18: Covariant Derivative (extrinsic) and Parallel Transport
First video on Covariant Derivative in flat space: https://www.youtube.com/watch?v=U5iMpOn5IHw ERROR at 21:00, the 1st line, there should also be a (partial ...
eigenchris
Implicit Function Theorem
Differential Calculus in Several Variables
Calculus on Manifolds for Thermodynamics Part 1.wmv
UPDATED OCT 9 2013: Manifolds used in Thermodynamics as state spaces of thermodynamic systems differ from those we study in vector calculus. There is no ...
Mathview
44 - Proof of the implicit function theorem
Calculus 2 - international Course no. 104004 Dr. Aviv Censor Technion - International school of engineering.
Technion
Curvature: Intuition and Derivation | Differential Geometry
In my 5th video on #DifferentialGeometry, I define the #Curvature for both a unit speed curve reparametrized with respect to arc length and a regular curve ...
Faculty of Khan
2. Introduction to tensors.
MIT 8.962 General Relativity, Spring 2020 Instructor: Scott Hughes View the complete course: https://ocw.mit.edu/8-962S20 YouTube Playlist: ...
MIT OpenCourseWare
Tensor Calculus 6: Differential Forms are Covectors
Tensors for Beginners: What are Covectors: https://www.youtube.com/watch?v=LNoQ_Q5JQMY.
eigenchris
Rotation Averaging and Optimization on Manifolds
I will discuss averaging on manifolds, mainly the manifold SO3 of 3D rotations. A number of theoretical results will be given, in particular conditions for convexity ...
Microsoft Research
Manifolds, classification of surfaces and Euler characteristic | Differential Geometry 25
Here we give an informal introduction to the modern idea of `manifold', putting aside all the many logical difficulties that are bound up in this definition: difficulties ...
Insights into Mathematics
Arc Length and Reparameterization | Differential Geometry 2
In this video, I continue my series on Differential Geometry with a discussion on arc length and reparametrization. I begin the video by talking about arc length, ...
Faculty of Khan
Tensor Calculus 16: Geodesic Examples on Plane and Sphere
Previous Video (15) on Geodesics: https://www.youtube.com/edit?o=U&video_id=1CuTNveXJRc Video 12 on the Sphere metric: ...
eigenchris
Tangent spaces and Riemannian manifolds
In this video, we give three alternative ways to view tangent vectors on manifolds. The first is dynamic, viewing tangent vectors as velocities of trajectories, the ...
DanielChanMaths
Laplacian intuition
A visual understanding for how the Laplace operator is an extension of the second derivative to multivariable functions.
Khan Academy
Mod-15 Lec 41 Any Variety is a Smooth Manifold with or without Non-Smooth Boundary
nptelhrd
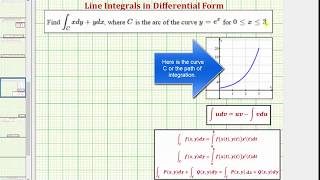
Evaluate a Line Integral of in Differential Form
This video explains how to evaluate a line integral in differential form. http://mathispower4u.com.
Mathispower4u
A Look at Some Higher Level Math Classes | Getting a Math Minor
STEMerch Store: https://stemerch.com/ Support the Channel: https://www.patreon.com/zachstar PayPal(one time donation): https://www.paypal.me/ZachStarYT ...
Zach Star
Beltrami Identity Derivation | Calculus of Variations
After 1 month of self-imposed exile to Med School Island (my apologies for the long wait btw), I'm finally back with a video! This time, I've made a tutorial on ...
Faculty of Khan
Tensor Calculus Lecture 8: Embedded Surfaces and the Curvature Tensor
This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: ...
MathTheBeautiful
Michael Hopkins: Bernoulli numbers, homotopy groups, and Milnor
Abstract: In his address at the 1958 International Congress of Mathematicians Milnor described his joint work with Kervaire, relating Bernoulli numbers, ...
The Abel Prize
More general surfaces | Differential Geometry 22 | NJ Wildberger
This video follows on from DiffGeom21: An Introduction to surfaces, starting with ruled surfaces. These were studied by Euler, and Monge gave examples of how ...
Insights into Mathematics
Ursula HAMENSTÄDT - The geometry of 3 - manifolds before and after Perelman
The rank of a hyperbolic manifold is the smallest number of generators of its fundamental group. McMullen conjectured that for all $k\geq 2$, the pointwise ...
Institut des Hautes Études Scientifiques (IHÉS)
Advanced Calculus: abstract manifolds, differentiation, 9-29-17, part 1
James Cook
The Most Famous Calculus Book in Existence "Calculus by Michael Spivak"
The Most Famous Calculus Book in Existence "Calculus by Michael Spivak" Link to book on amazon is: https://amzn.to/2WcHB5T (note this is my affiliate link, ...
The Math Sorcerer
Discrete Differential Geometry - Lecture 18: The Laplace Operator
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg.
Keenan Crane
The Simple Essence of Automatic Differentiation - Conal Elliott
Automatic differentiation (AD) in reverse mode (RAD) is a central component of deep learning and other uses of large-scale optimization. Commonly used RAD ...
Microsoft Research
Worldwide Calculus: Parameterizing Surfaces
Lecture on 'Parameterizing Surfaces' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
Center of Math
Multivariable Calculus: Calculus in 4 Dimensions
At the end of a multivariable course we are often asked what calculus is like beyond 3 dimensions. This is an attempt to outline multi-variable calculus in four ...
Oliver Knill
Shifrin Math 3510 Day40: Proof of Stokes' Theorem, part 1
Dr. Theodore Shifrin, professor at the University of Georgia, presents material from his textbook: Multivariable Mathematics: Linear Algebra, Multivariable ...
Math 3500/10