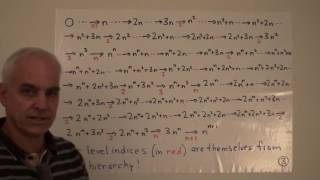The Discrete Charm of Geometry by Alexander Bobenko
Kaapi with Kuriosity The Discrete Charm of Geometry Speaker: Alexander Bobenko (Technical University of Berlin) When: 4pm to 6pm Sunday, 22 July 2018 ...
International Centre for Theoretical Sciences
Simple New Projective Geometry Axioms
In this video I introduce a new axiomatic framework for the projective plane which does not require the notions or points and lines. The system is inspired by the ...
Richard Southwell
Visualizing Hyperspace Via Projective Geometry
We introduce the idea of high dimensional space using simple pictures, and then proceed to examine many projective issues upon it. When considering ...
Richard Southwell
The projective line, circles and the CQQ theorem (II) | Rational Geometry Math Foundations 130
We extend our proof of the Cyclic quadrilateral quadrea theorem to general circles in the plane. This requires us first of all to discuss general circles.
Insights into Mathematics
Bretschneider Theorem/formula | How to easily derive the Bretschneider Theorem hindi | Kamaldheeriya
In this video proof of Bretschneider's theorem, which states that if s = (a+b+c+d)/2 and A and C are opposing angles in the quadrilateral, then the area of the ...
Kamaldheeriya Maths easy
Absolute versus relative measurements in geometry | Rational Geometry Math Foundations 134
In science and ordinary life, the distinction between absolute and relative measurements is very useful. It turns out that in mathematics this is also an important ...
Insights into Mathematics
FPG8 One Dimensional Projections, Involutions
In this lecture we discuss the three different types of one dimensional projectivities, and how these relate to the central topic of harmonic sets. After discussing ...
Richard Southwell
Relativistic velocity, core circles, and Paul Miller's protractor (II) | Rational Geometry MF143
We introduce an important variant to the unit circle---what we call the core circle, which has diameter the unit interval [0,1]. For understanding the projective line, ...
Insights into Mathematics
Complex Numbers and Addition Formulas | Algebraic Calculus One | Wild Egg
Circle geometry and related formulas in calculus are closely connected to the algebra of complex numbers. In particular the all-important rational parametrization ...
Wild Egg mathematics courses
Lecture 2: Topological Manifolds (International Winter School on Gravity and Light 2015)
As part of the world-wide celebrations of the 100th anniversary of Einstein's theory of general relativity and the International Year of Light 2015: Central lecture ...
The WE-Heraeus International Winter School on Gravity and Light
Polarities At The Foundations Of Geometry
The idea of polarities is one of the most revealing notions in geometry. The forms of the conic section curves themselves can be thought of as emerging from ...
Richard Southwell
Bretschneider Theorem/formula to Brahmagupta Formula and Heron's Formula easily | Kamaldheeriya
In this video proof of Bretschneider's theorem, which states that if s = (a+b+c+d)/2 and A and C are opposing angles in the quadrilateral, then the area of the ...
Kamaldheeriya Maths easy
Damian Rössler: The arithmetic Riemann Roch Theorem and Bernoulli numbers
The lecture was held within the framework of the Hausdorff Trimester Program: Periods in Number Theory, Algebraic Geometry and Physics. Abstract: (with V.
Hausdorff Center for Mathematics
MF150: What exactly is a set? | Data Structures in Mathematics Math Foundations | NJ Wildberger
What exactly is a set?? This is a crucial question in the modern foundations of mathematics. Here we begin an examination of this thorny issue, first by ...
Insights into Mathematics
The successor-limit hierarchy and ordinals II | Data structures Math Foundations 183
This video is a continuation of MF181, in which we reviewed and extended the successor-limit hierarchy of very big arithmetical operations. In this video we want ...
Insights into Mathematics
Hyperoperations and even bigger numbers | Data structures in Mathematics Math Foundations 179
A powerful approach to exploring big number arithmetic is to extend the notion of arithmetical operation. By considering hyperoperations starting with +,x,^ and ...
Insights into Mathematics
The realm of natural number multisets | Data structures in Mathematics Math Foundations 156
We introduce the realm of natural number multisets Mset(n) for a fixed natural number n. Such msets are k-msets from n, where k is now allowed to be variable.
Insights into Mathematics
Sets and other data structures | Data Structures in Mathematics Math Foundations 151
In mathematics we often want to organize objects. Sets are not the only way of doing this: there are other data types that are also useful and that can be ...
Insights into Mathematics
Multisets and a new framework for arithmetic | Data Structures Math Foundations 187
Here we go back to the first videos in this series and recast that discussion in a more solid direction by utilizing our understanding of multisets. The crucial point ...
Insights into Mathematics
The projective Triple Quad Formula | Rational Geometry Math Foundations 136 | NJ Wildberger
Here we establish the projective analog of the (affine) Triple quad formula. This tells us the relationship between the three projective quadrances formed by three ...
Insights into Mathematics
NJ's pizza model for organizing geometry | Rational Geometry Math Foundations 135 | NJ Wildberger
How do we organize metrical geometry? This video gives a broad outline of the subject---using a close parallel with how you might make a pizza. Just as there ...
Insights into Mathematics
The rational number line and irrationalities (b) | Famous Math Problems 19b | NJ Wildberger
In this video we present a basic and profound solution to the most important and fundamental problem in mathematics (which is: How to model the continuum?)
Insights into Mathematics
Solving Triangles with Rational Trigonometry | WildTrig: Intro to Rational Trigonometry
Shows how to solve triangles using the framework of rational trigonometry with quadrances and spreads replacing distance and angle. A screenshot PDF which ...
Insights into Mathematics
Limit levels + self-similarity in successor-limit hierarchy | Data structures Math Foundations 184
The successor - limit hierarchy exhibits interesting kinds of self-similarity, along the lines of fractals. One manifestation of this appears when we look at the levels ...
Insights into Mathematics
Number systems and Stevin's decimals | Math History | NJ Wildberger
We review some of the development of number systems from the ancient Greeks, followed by the Indian and then Arabic development of our Hindu-Arabic ...
Insights into Mathematics
The law of logical honesty and the end of infinity | Data structures in Math Foundations 178
It is time to end the delusion which pervades modern 20th century style mathematics, and move towards a true mathematics for the new millennium. Infinity ...
Insights into Mathematics
Fun with lists, ordered sets, multisets I Data Structures in Mathematics Math Foundations 152
In our last video we introduced four types of concrete data structures that we could build using natural numbers: k-lists, k-ordered sets, k-multiset and k-sets.
Insights into Mathematics
The story of Yvo Staudt - Staudt Watches
Yvo Staudt his dream was to become a classical accordion player. He ended up with his own watch brand. He tells how. Discover our full story at our website: ...
Staudt Watches
Karl Georg Christian von Staudt
If you find our videos helpful you can support us by buying something from amazon. https://www.amazon.com/?tag=wiki-audio-20 Karl Georg Christian von ...
WikiAudio
Unique factorization, primes and msets | Data Structures in Mathematics Math Foundations 160
We look at some elementary number theory from the view of applying what we have learned about multisets, including the somewhat novel idea of ...
Insights into Mathematics
Joachim Staudt: Northern Sun (from the album: Seven Wishes)
Die CD direkt bei mir bestellen: http://www.joachimstaudt.com Order the album here: http://www.joachimstaudt.com.
Joachim Staudt
Fun with lists, multisets and sets III | Data Structures in Mathematics Math Foundations 154
We continue our discussion of data structures in mathematics, now treating the case of multisets or msets. This is an unordered structure in which repetitions are ...
Insights into Mathematics
Numbers, the universe and complexity beyond us | Data structures Math Foundations 177
In mathematics, we want to write things down. That way we can check what we are actually talking about. Other people can look at it, and assess whether it ...
Insights into Mathematics
Construction of Quadrilaterals | ikenSchool
This video explains about construction of a quadrilateral while some conditions or information is provided like four sides and one diagonal is given, two sides ...
ikenschool
Deep Order Mathematics: Nature of the 'Mental'
The Mental is posited as having 4 layers to it. Each of these layers is defined by an equation or set and the hypothesis is that the outer layer is gradually ...
Pravir Malik
What is SCREW THEORY? What does SCREW THEORY mean? SCREW THEORY meaning, definition & explanation
http://www.theaudiopedia.com What is SCREW THEORY? What does SCREW THEORY mean? SCREW THEORY meaning - SCREW THEORY ...
The Audiopedia
Jewelry Party Wednesday: Boho Chic & Fancy Free
Veronica Staudt
Mod-01 Lec-25 Ganitakaumudi of Narayana Pandita 1
Mathematics in India - From Vedic Period to Modern Times by Prof. M.D.Srinivas,Prof.M.S.Sriram & Prof.K.Ramasubramanian,Department of mathematics,IIT ...
nptelhrd
Deep Order Mathematics: Enhancing the Equation of the 'Mental'
We review the four layers of the Mental equation subject to the action of the Transformation Circle (TC) to arrive at the conditions of movement from one layer to ...
Pravir Malik
Complex projective space | Wikipedia audio article
This is an audio version of the Wikipedia Article: https://en.wikipedia.org/wiki/Complex_projective_space 00:00:52 1 Introduction 00:03:58 2 Construction ...
wikipedia tts
Finite geometry | Wikipedia audio article
This is an audio version of the Wikipedia Article: https://en.wikipedia.org/wiki/Finite_geometry 00:01:26 1 Finite planes 00:02:04 1.1 Finite affine planes 00:04:01 ...
wikipedia tts
How to Teach Area of a Quadrilateral
Area is the amount of space that takes up the surface of an object. Learn how to teach your child to measure area. Find more videos and resources that go ...
My LearningBlock